

Next: アルゴリズム
Up: 粒子群最適化(Particle Swarm Optimization)
Previous: 粒子群最適化(Particle Swarm Optimization)
エージェントのグループがある目的関数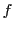 を最適化すると仮定する.
各エージェント
を最適化すると仮定する.
各エージェント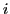 は,時刻
は,時刻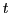 における各自の位置
における各自の位置
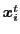 ,移動速度
,移動速度
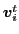 ,および今まで経験した目的関数の最良値
,および今まで経験した目的関数の最良値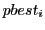 とそのときの位置
とそのときの位置
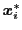 を記憶している.
を記憶している.
さらに,各エージェントは,グループ中のエージェントが経験した目的関数の最良値 とそのときの位置
とそのときの位置
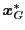 の情報を共有する.
の情報を共有する.
このとき,時刻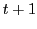 におけるエージェントの移動速度は,以下のように求められる.
におけるエージェントの移動速度は,以下のように求められる.
ただし,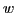 は慣性重み(inertia weight),
は慣性重み(inertia weight),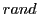 は区間
は区間![$[0,1]$](img34.png) の一様乱数であり,各成分毎に生成する.
の一様乱数であり,各成分毎に生成する.
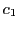 は``cognitive'',
は``cognitive'',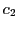 は``social''とよばれるパラメータであり,自己の最良位置およびグループの最良位置への探索に対する重み付けを表現している.
は``social''とよばれるパラメータであり,自己の最良位置およびグループの最良位置への探索に対する重み付けを表現している.
式(7)から,時刻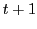 におけるエージェントの位置が以下のように求められる.
におけるエージェントの位置が以下のように求められる.
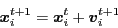 |
(8) |
takahama
2007-07-13
![]() におけるエージェントの位置が以下のように求められる.
におけるエージェントの位置が以下のように求められる.