

Next: 粒子群最適化(Particle Swarm Optimization)
Up: 差分進化
Previous: 定義
DE/rand/1/{bin,exp} のアルゴリズムは以下のように記述できる[3,4].
- Step0
- 初期化.
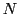 個の初期個体
個の初期個体
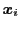 を初期探索点として生成し,初期集団
を初期探索点として生成し,初期集団
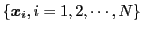 を構成する.
全ての個体を評価する.
を構成する.
全ての個体を評価する.
- Step1
- 終了判定.
終了条件を満足すれば,アルゴリズムは終了する.終了条件としては,最大の繰り返し回数や関数評価回数を用いることが多い.
- Step2
- 突然変異.
各個体
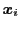 に対して,3個体
に対して,3個体
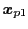 ,
,
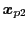 ,
,
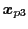 を
を
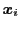 および互いに重複しないようにランダムに選択する.
新しいベクトル
および互いに重複しないようにランダムに選択する.
新しいベクトル
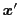 を基本ベクトル
を基本ベクトル
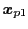 および差分ベクトル
および差分ベクトル
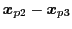 から以下のように生成する.
から以下のように生成する.
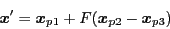 |
(2) |
ここで,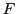 はスケーリングパラメータである.
はスケーリングパラメータである.
- Step3
- 交叉.
ベクトル
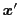 を親
を親
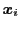 と交叉し,子ベクトル
と交叉し,子ベクトル
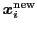 を生成する.
交差点
を生成する.
交差点 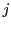 を全ての次元
を全ての次元 ![$[1,n]$](img29.png) からランダムに選択する.
子ベクトル
からランダムに選択する.
子ベクトル
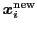 の
の 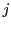 番目の要素を
番目の要素を
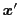 の
の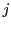 番目の要素から継承する.
交叉法がbinの場合には,それ以降の次元は,交叉率
番目の要素から継承する.
交叉法がbinの場合には,それ以降の次元は,交叉率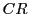 の確率で,
の確率で,
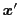 の要素から継承し,
の要素から継承し,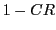 の確率で親
の確率で親
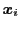 から継承する.
交叉法がexpの場合には,それ以降の次元は,
から継承する.
交叉法がexpの場合には,それ以降の次元は,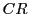 によって指数関数的に減少する確率で,
によって指数関数的に減少する確率で,
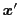 の要素から継承し,残りの部分は,親
の要素から継承し,残りの部分は,親
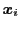 から継承する.
実際の処理では,Step2 と Step3 は一まとまりの処理で実現される.
から継承する.
実際の処理では,Step2 と Step3 は一まとまりの処理で実現される.
- Step4
- ポテンシャル法.もし,子ベクトルが親ベクトルよりも良いと推定されれば,Step5に進む.そうでなければ,Step6 に進む.
- Step5
- 生存者選択.
子ベクトルを評価する.
子ベクトル
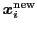 が親ベクトルよりも良ければ子ベクトルが生存者となり,親を子ベクトルで置換する.
が親ベクトルよりも良ければ子ベクトルが生存者となり,親を子ベクトルで置換する.
- Step6
- Step1 に戻る.
以下に擬似コードを示す.
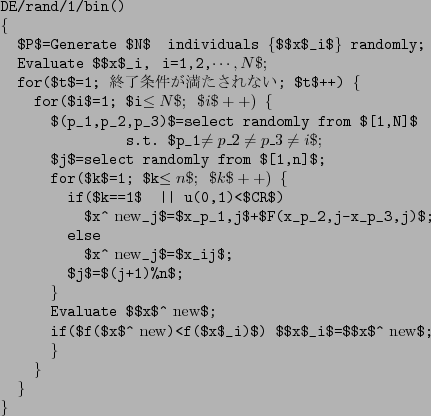
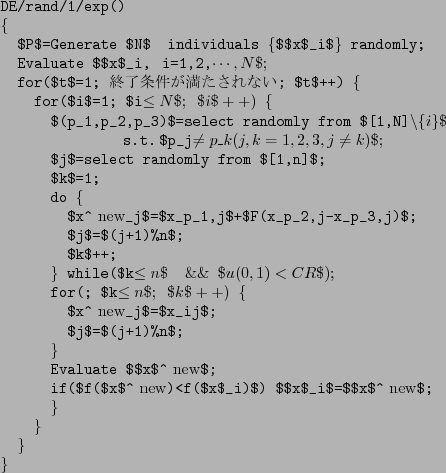
ここで,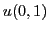 は区間
は区間![$[0,1]$](img34.png) の一様乱数生成関数である.
の一様乱数生成関数である.
takahama
2007-07-13


![]() は区間
は区間![]() の一様乱数生成関数である.
の一様乱数生成関数である.