

Next: 集団的降下法
Up: 最適化問題と集団的降下法
Previous: 最適化問題と集団的降下法
一般的な最適化問題(P)は,不等式制約,等式制約,上下限制約を有しており,以下のように定義できる.
![$\displaystyle \arraycolsep=1mm
(P)
\begin{array}[t]{ll}
\mbox{minimize} & f(\mb...
...$}) = 0,\; j=q+1, \dots, m \\
& l_i \le x_i \le u_i,\; i=1,\dots,n
\end{array}$](img1.png) |
|
|
(1) |
ここで,
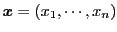 は
は 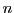 次元決定変数ベクトル,
次元決定変数ベクトル,
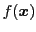 は目的関数,
は目的関数,
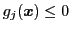 は
は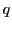 個の不等式制約,
個の不等式制約,
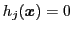 は
は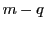 個の等式制約であり,
個の等式制約であり,
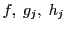 は線形あるいは非線形の実数値関数である.
は線形あるいは非線形の実数値関数である.
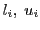 はそれぞれ,
はそれぞれ,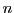 個の決定変数
個の決定変数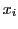 の下限値,上限値である.
の下限値,上限値である.
目的関数および制約条件がともに線形の場合が線形計画問題,その他の場合が非線形計画問題である.
ここでは,不等式制約および等式制約のない問題の最適化について説明する.
takahama
2007-07-13
![$\displaystyle \arraycolsep=1mm
(P)
\begin{array}[t]{ll}
\mbox{minimize} & f(\mb...
...$}) = 0,\; j=q+1, \dots, m \\
& l_i \le x_i \le u_i,\; i=1,\dots,n
\end{array}$](img1.png)
![$\displaystyle \arraycolsep=1mm
(P)
\begin{array}[t]{ll}
\mbox{minimize} & f(\mb...
...$}) = 0,\; j=q+1, \dots, m \\
& l_i \le x_i \le u_i,\; i=1,\dots,n
\end{array}$](img1.png)